15.3. Refactoring

The best thing about comprehensive unit testing is not the feeling you get when all your test cases finally pass, or even the feeling you get when someone else blames you for breaking their code and you can actually prove that you didn't. The best thing about unit testing is that it gives you the freedom to refactor mercilessly.

Refactoring is the process of taking working code and making it work better. Usually, “better” means “faster”, although it can also mean “using less memory”, or “using less disk space”, or simply “more elegantly”. Whatever it means to you, to your project, in your environment, refactoring is important to the long-term health of any program.

Here, “better” means “faster”. Specifically, the fromRoman function is slower than it needs to be, because of that big nasty regular expression that you use to validate Roman numerals. It's probably not worth trying to do away with the regular expression altogether (it would be difficult, and it might not end up any faster), but you can speed up the function by precompiling the regular expression.

Example 15.10. Compiling regular expressions

>>> import re
>>> pattern = '^M?M?M?$'
>>> re.search(pattern, 'M')               1
<SRE_Match object at 01090490>
>>> compiledPattern = re.compile(pattern) 2
>>> compiledPattern
<SRE_Pattern object at 00F06E28>
>>> dir(compiledPattern)                  3
['findall', 'match', 'scanner', 'search', 'split', 'sub', 'subn']
>>> compiledPattern.search('M')           4
<SRE_Match object at 01104928>
1 This is the syntax you've seen before: re.search takes a regular expression as a string (pattern) and a string to match against it ('M'). If the pattern matches, the function returns a match object which can be queried to find out exactly what matched and how.
2 This is the new syntax: re.compile takes a regular expression as a string and returns a pattern object. Note there is no string to match here. Compiling a regular expression has nothing to do with matching it against any specific strings (like 'M'); it only involves the regular expression itself.
3 The compiled pattern object returned from re.compile has several useful-looking functions, including several (like search and sub) that are available directly in the re module.
4 Calling the compiled pattern object's search function with the string 'M' accomplishes the same thing as calling re.search with both the regular expression and the string 'M'. Only much, much faster. (In fact, the re.search function simply compiles the regular expression and calls the resulting pattern object's search method for you.)
Note
Whenever you are going to use a regular expression more than once, you should compile it to get a pattern object, then call the methods on the pattern object directly.

Example 15.11. Compiled regular expressions in roman81.py

This file is available in py/roman/stage8/ in the examples directory.

If you have not already done so, you can download this and other examples used in this book. 

# toRoman and rest of module omitted for clarity

romanNumeralPattern = \
    re.compile('^M?M?M?M?(CM|CD|D?C?C?C?)(XC|XL|L?X?X?X?)(IX|IV|V?I?I?I?)$') 1

def fromRoman(s):
    """convert Roman numeral to integer"""
    if not s:
        raise InvalidRomanNumeralError, 'Input can not be blank'
    if not romanNumeralPattern.search(s):                                    2
        raise InvalidRomanNumeralError, 'Invalid Roman numeral: %s' % s

    result = 0
    index = 0
    for numeral, integer in romanNumeralMap:
        while s[index:index+len(numeral)] == numeral:
            result += integer
            index += len(numeral)
    return result
1 This looks very similar, but in fact a lot has changed. romanNumeralPattern is no longer a string; it is a pattern object which was returned from re.compile.
2 That means that you can call methods on romanNumeralPattern directly. This will be much, much faster than calling re.search every time. The regular expression is compiled once and stored in romanNumeralPattern when the module is first imported; then, every time you call fromRoman, you can immediately match the input string against the regular expression, without any intermediate steps occurring under the covers.

So how much faster is it to compile regular expressions? See for yourself:

Example 15.12. Output of romantest81.py against roman81.py

.............          1
----------------------------------------------------------------------
Ran 13 tests in 3.385s 2

OK                     3
1 Just a note in passing here: this time, I ran the unit test without the -v option, so instead of the full docstring for each test, you only get a dot for each test that passes. (If a test failed, you'd get an F, and if it had an error, you'd get an E. You'd still get complete tracebacks for each failure and error, so you could track down any problems.)
2 You ran 13 tests in 3.385 seconds, compared to 3.685 seconds without precompiling the regular expressions. That's an 8% improvement overall, and remember that most of the time spent during the unit test is spent doing other things. (Separately, I time-tested the regular expressions by themselves, apart from the rest of the unit tests, and found that compiling this regular expression speeds up the search by an average of 54%.) Not bad for such a simple fix.
3 Oh, and in case you were wondering, precompiling the regular expression didn't break anything, and you just proved it.

There is one other performance optimization that I want to try. Given the complexity of regular expression syntax, it should come as no surprise that there is frequently more than one way to write the same expression. After some discussion about this module on comp.lang.python, someone suggested that I try using the {m,n} syntax for the optional repeated characters.

Example 15.13. roman82.py

This file is available in py/roman/stage8/ in the examples directory.

If you have not already done so, you can download this and other examples used in this book. 

# rest of program omitted for clarity

#old version
#romanNumeralPattern = \
#   re.compile('^M?M?M?M?(CM|CD|D?C?C?C?)(XC|XL|L?X?X?X?)(IX|IV|V?I?I?I?)$')

#new version
romanNumeralPattern = \
    re.compile('^M{0,4}(CM|CD|D?C{0,3})(XC|XL|L?X{0,3})(IX|IV|V?I{0,3})$')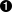 1
1 You have replaced M?M?M?M? with M{0,4}. Both mean the same thing: “match 0 to 4 M characters”. Similarly, C?C?C? became C{0,3} (“match 0 to 3 C characters”) and so forth for X and I.

This form of the regular expression is a little shorter (though not any more readable). The big question is, is it any faster?

Example 15.14. Output of romantest82.py against roman82.py

.............
----------------------------------------------------------------------
Ran 13 tests in 3.315s 1

OK                     2
1 Overall, the unit tests run 2% faster with this form of regular expression. That doesn't sound exciting, but remember that the search function is a small part of the overall unit test; most of the time is spent doing other things. (Separately, I time-tested just the regular expressions, and found that the search function is 11% faster with this syntax.) By precompiling the regular expression and rewriting part of it to use this new syntax, you've improved the regular expression performance by over 60%, and improved the overall performance of the entire unit test by over 10%.
2 More important than any performance boost is the fact that the module still works perfectly. This is the freedom I was talking about earlier: the freedom to tweak, change, or rewrite any piece of it and verify that you haven't messed anything up in the process. This is not a license to endlessly tweak your code just for the sake of tweaking it; you had a very specific objective (“make fromRoman faster”), and you were able to accomplish that objective without any lingering doubts about whether you introduced new bugs in the process.

One other tweak I would like to make, and then I promise I'll stop refactoring and put this module to bed. As you've seen repeatedly, regular expressions can get pretty hairy and unreadable pretty quickly. I wouldn't like to come back to this module in six months and try to maintain it. Sure, the test cases pass, so I know that it works, but if I can't figure out how it works, it's still going to be difficult to add new features, fix new bugs, or otherwise maintain it. As you saw in Section 7.5, “Verbose Regular Expressions”, Python provides a way to document your logic line-by-line.

Example 15.15. roman83.py

This file is available in py/roman/stage8/ in the examples directory.

If you have not already done so, you can download this and other examples used in this book. 

# rest of program omitted for clarity

#old version
#romanNumeralPattern = \
#   re.compile('^M{0,4}(CM|CD|D?C{0,3})(XC|XL|L?X{0,3})(IX|IV|V?I{0,3})$')

#new version
romanNumeralPattern = re.compile('''
    ^                   # beginning of string
    M{0,4}              # thousands - 0 to 4 M's
    (CM|CD|D?C{0,3})    # hundreds - 900 (CM), 400 (CD), 0-300 (0 to 3 C's),
                        #            or 500-800 (D, followed by 0 to 3 C's)
    (XC|XL|L?X{0,3})    # tens - 90 (XC), 40 (XL), 0-30 (0 to 3 X's),
                        #        or 50-80 (L, followed by 0 to 3 X's)
    (IX|IV|V?I{0,3})    # ones - 9 (IX), 4 (IV), 0-3 (0 to 3 I's),
                        #        or 5-8 (V, followed by 0 to 3 I's)
    $                   # end of string
    ''', re.VERBOSE)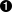 1
1 The re.compile function can take an optional second argument, which is a set of one or more flags that control various options about the compiled regular expression. Here you're specifying the re.VERBOSE flag, which tells Python that there are in-line comments within the regular expression itself. The comments and all the whitespace around them are not considered part of the regular expression; the re.compile function simply strips them all out when it compiles the expression. This new, “verbose” version is identical to the old version, but it is infinitely more readable.

Example 15.16. Output of romantest83.py against roman83.py

.............
----------------------------------------------------------------------
Ran 13 tests in 3.315s 1

OK                     2
1 This new, “verbose” version runs at exactly the same speed as the old version. In fact, the compiled pattern objects are the same, since the re.compile function strips out all the stuff you added.
2 This new, “verbose” version passes all the same tests as the old version. Nothing has changed, except that the programmer who comes back to this module in six months stands a fighting chance of understanding how the function works.

<< Handling changing requirements
 | 1 | 2 | 3 | 4 | 5 | 
Postscript >>

Copyright © 2023 Mark Pilgrim, diveintopython.org